Crosswind Formula Explained
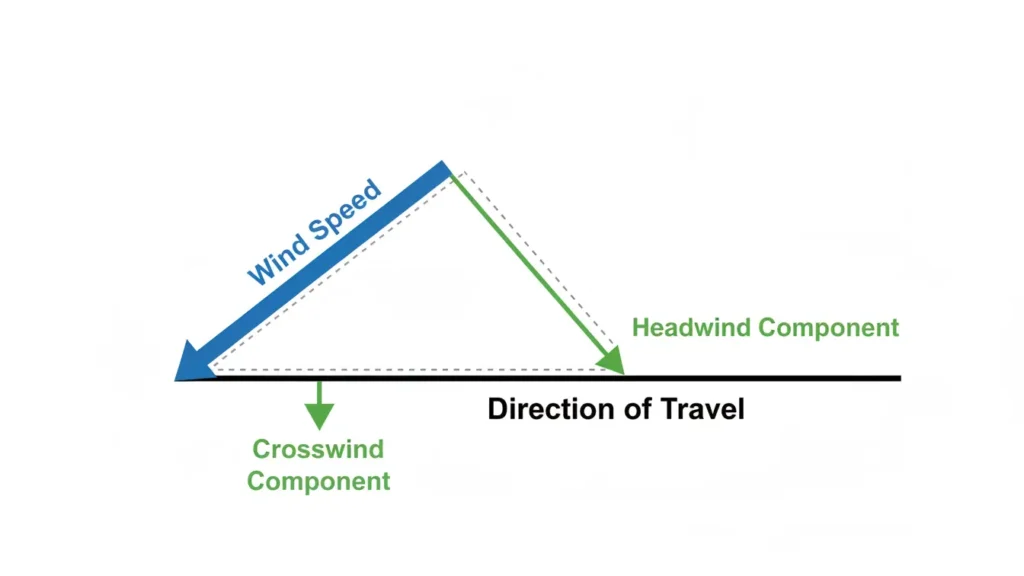
When people hear the phrase crosswind calculation formula, they often expect complex math. In reality, the idea behind the formula is simple. The challenge is not the calculation itself, but understanding what part of the wind actually affects your direction of travel.
This page explains the exact mathematical formula used to calculate crosswind. It is designed for readers who want to see the actual equations behind the calculator and understand how wind direction and speed translate into sideways force. This formula is based on basic vector projection principles used in navigation, physics, and engineering calculations.
Formula Used to Calculate the Crosswind Component
The crosswind component is calculated using the sine of the angle between the wind direction and the direction of travel.
Crosswind Component = Wind Speed × sin(θ)
Where:
- Wind Speed is the total wind velocity
- θ (theta) is the angle between wind direction and direction of travel
- sin(θ) represents the perpendicular portion of the wind force
This formula extracts only the sideways force created by angled wind.
Why the Sine Function Is Used?
Sine is used because it calculates the perpendicular component of a force.
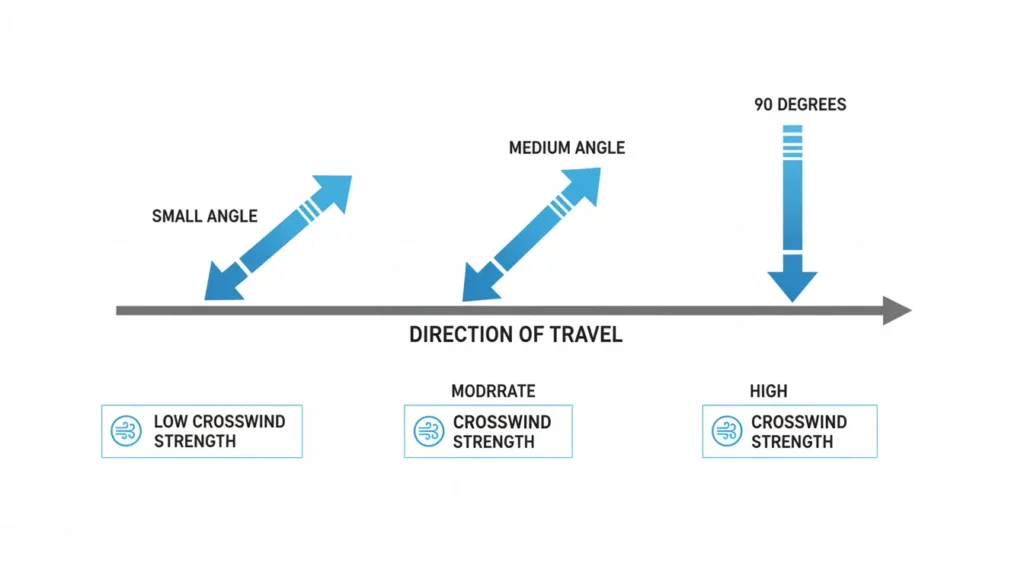
When wind is aligned with the direction of travel, θ = 0°, and sin(0°) = 0. This produces no crosswind.
As the wind angle increases, the sine value increases. At 90°, sin(90°) = 1, meaning the entire wind speed acts as crosswind.
Example Crosswind Calculation:
If the wind speed is 20 knots and the wind approaches at a 30-degree angle to the direction of travel, the crosswind component is calculated as:
Crosswind = 20 × sin(30°)
Since sin(30°) equals 0.5, the resulting crosswind component is 10 knots.
This shows how even moderate wind speeds can create noticeable sideways force when the angle increases.
This behavior matches real-world physics, which is why sine is the correct function for crosswind calculation.
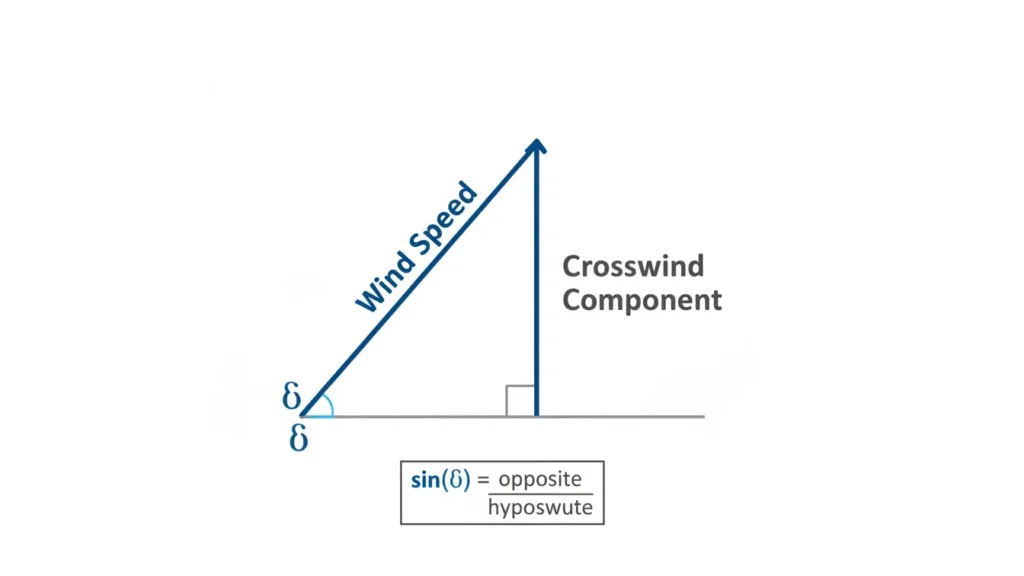
Headwind and Tailwind Formula
The headwind or tailwind component is calculated using the cosine of the same angle.
Formula:
Headwind Component = Wind Speed × cos(θ)
Where:
- A positive result indicates a headwind
- A negative result indicates a tailwind
Cosine isolates the parallel component of the wind instead of the sideways component. Together, sine and cosine split wind force into perpendicular and parallel components without overlap.
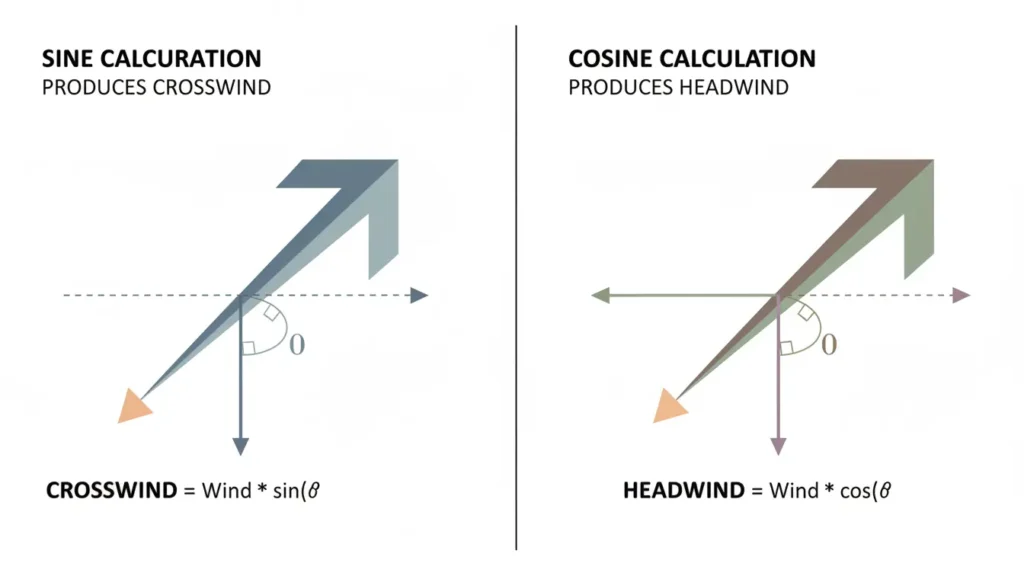
What the Formula Measures and What It Does Not
The crosswind calculation formula measures only directional force based on geometry.
It does not account for:
- Gust intensity
- Surface conditions
- Vehicle or aircraft handling technique
This is intentional. The formula provides a consistent baseline that reflects how wind direction and speed interact mathematically. This separation ensures the formula remains consistent and predictable regardless of surface conditions or vehicle type.
Why the Formula Always Produces Consistent Results?
The formula is deterministic. Given the same wind speed and angle, the result will always be the same.
This consistency exists because the formula follows vector projection principles. It does not rely on estimation, charts, or experience-based judgment.
This is why the same formula is used across calculators, planning tools, and reference charts.
How Calculators Apply the Formula Instantly
Crosswind calculators use the same formula but apply it automatically.
Instead of manually calculating angles or sine values, the calculator performs the computation instantly and displays the result visually.
If you want to see this formula working in real time, use the crosswind calculator on this site. This consistency exists because the formula follows vector projection principles. It does not rely on estimation, charts, or experience-based judgment.
Summary
The crosswind calculation formula isolates the sideways force created when wind approaches at an angle. By multiplying wind speed by the sine of the wind angle, the formula accurately measures how much wind acts perpendicular to the direction of travel. This mathematical relationship mirrors real-world behavior and provides reliable, repeatable results.